BQ #7:Unit V

 Difference Quotient

The difference quotient is a formula that finds the slope of the secant line and will help us find the slope of any given slope of a tangent line. Since the difference quotient is used for the slope, it is derived from the slope formula.

Using the slope formula of y2-y1/x2-x1, we know that the x1 and y1 is just x because that is our first point on the graph.The second point is unknown so it is x + the change in height which is h, (x+h). We now plug in the (x+h) for x2 and y2. This gives us (x+h)-y1/(x+h)-x1. In the denominator we have the x's canceling and that would leave us with (x+h)-y/h. Or (x+h)-x/h. This is how we derive the difference quotient from the slope formula.

http://s2.hubimg.com/u/5678981_f520.jpg

http://upload.wikimedia.org/wikipedia/commons/8/8c/Derivative.png

BQ #6: Unit U

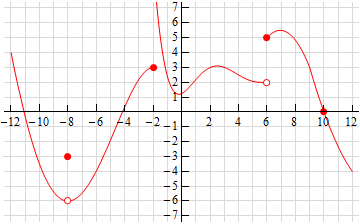
1. What is continuity? And what is discontinuity?

A continuity is a function in which on a graph is predictable, has no breaks, no holes, and no jumps, and can be drawn without lifting your pencil. While a discontinuity is the opposite, it isn't predictable, has breaks, holes, and jumps, and you must lift your pencil to draw these. A discontinuity are set in two families: removable and non removable. These are different and it will be mentioned later in this post.  In the removable discontinuities there is only one and that is the point discontinuity, this is usually known as a hole. In the non removable discontinuities there are three; the jump, oscillating, and infinite discontinuities. The jump discontinuity is when it goes from one point on a graph to another without the graph touching. An oscillating discontinuity is when the graph just becomes a bunch of wiggly lines. The infinite discontinuity is a result of a vertical asymptote.

2. What is a limit?

A limit is the intended height of a graph. The limit exists when we reach the same height from the left and right. This can only be reached if the graph is a continuity or part of the removable discontinuities. There will be no limit if the non removable discontinuities are set. With this, the limit will not exist when the graph is different from the left and the right, when there is unbounded behavior, and/or there is oscillating behavior. A limit is different from a value because the limit is only the predicted point of a function, while the value is the actual point of the function.

3. How do we evaluate limits? 

To evaluate the limit numerically we must set up a table. In this table we have the x we approach as our middle number and we get as close to that number as possible from the left and right, usually with .1, .01, .001 and .9, .99, .999. You plug the function into your calculator and trace the graph plugging in the numbers other than the middle number. To evaluate the limit graphically we must slide our fingers from the left and the right and when they get to the same height that approaches the x that is the limit. There are several ways to evaluate the limit algebraically with direct substitution, dividing out/factoring, and rationalizing/conjugate methods. In direct substitution we take the limit and plug it straight into the function. If the answer turns out to be a numerical value, 0/#, #/0 then those are the answers but if there is a 0/0 then you must look to use a different method. In factoring method, you factor both the numerator and the denominator and cancel the common terms. Once we cancel the terms we use direct substitution again for what is remaining. In the conjugate method we multiply the top and bottom by the conjugate of where usually the radical will be. When we multiply this it is just a different form of 1. So we multiply the conjugate and simplify it by foiling, but we do not multiply out the non conjugate. We do this because this is what will cancel out. After canceling our we go back to the substitution method. 

Conjugate method

http://hsmathelearnings4.wiki.hci.edu.sg/file/view/conjugate_example.jpg/204976568/328x342/conjugate_example.jpg

http://choosgs4math.wiki.hci.edu.sg/file/viewlimit_example_2.jpg/205241252/560x356/limit_example_2.jpg

http://tutorial.math.lamar.edu/problems/CalcI/Continuity_files/image002.gif

I/D1: Unit N

How do SRT and UC relate?

Inquiry Activity Summary:
In this activity we were asked to find and simplify the lengths of the special right triangles with the hypotenuse equalling 1. We must always draw the fortunate plane for each because the coordinate is derived from the unit circle.

30-60-90 SRT

Here we have the special right triangle of 30-60-90. This triangle has an original hypotenuse of (2x) a height of (x) and the length of (x rad 3). To make the hypotenuse of (2x) to equal 1 we must divide all sides of the triangle by (2x).

We divided all sides by 2x to reduce the hypotenuse equal to 1. The effect of doing this cause the length of the triangle to become rad 3/2. The height then becomes 1/2.

45-45-90 SRT

In this special right triangle we have the 45-45-90. The rules for this triangle we have the hypotenuse equal x rad 2 and both the height and length equal x.

To make the hypotenuse equal 1 we have to divide it by x rad 2. And whatever we do to one side we must do to all to keep it proportional. When we do this the height and length become rad 2/2.

60-30-90 SRT

This triangle is similar to the 30-60-90 triangle but it is in a different position. The hypotenuse is 2x the length is x and the height is x rad 3. We must do what we did to the first triangle and divide the sides by 2x.

When we divide by 2x the hypotenuse becomes 1, the length becomes 1/2, and the height is rad 3/2.

How does this activity help you to derive the Unit Circle?

This activity helps derive the unit circle because it helps us understand and know where the points of the unit circle come from. This activity also showed the way the triangles are proportioned so the hypotenuse is equal to one. 

5. 

The quadrants of the triangles shown are in quadrant one. The quadrants change the value of it is either positive or negative. In quadrant 2 x is negative and y is positive, in quadrant 3 x and y are negative, quadrant 4 x is positive and y is negative.

This triangle is in quadrant 2 and all x-values are negative.

In this it shows a triangle in quadrant and all values are negative.

This triangle is located in quadrant and all y values are negative in this quadrant.

INQUIRY ACTIVITY REFLECTION

The coolest thing I learned from this activity was that these triangles are the only ones that have these special rules.

This activity will help me in this unit because it will help me understand the unit circle and how the quadrants can affect the triangle and which points are positive and negative.

Something I never realized before about special right triangles and the unit circle is that the quadrant affects the negative and positive of a point. And that the triangles have special rules that only apply to these specific triangles.

BQ #4: Unit T Concept 3

• Why is a “normal” tangent graph uphill, but a “normal” Cotangent graph downhill? Use unit circle ratios to explain.
• 
• 
  
• A cotangent and tangent have goes different ways because of their ratios. Cotangent with x/y and tangent with y/x. These affect the graphs because it determines where the asymptotes will be. In a tangent graph when sine is 0 there will be an asymptote and when cosine is 0 there will be an asymptote for the cotangent graph. In the unit circle the quadrants are exactly the same but the ratio changes the graph. In quadrant 1 they are both positive but since sine is 0 at 90 degrees the tangent graph needs to go uphill in order to follow the unit circle of being positive and get near the asymptote. For the cotangent graph the asymptote is at 0 so the graph needs to start up near the asymptote to be positive then go downhill to be negative in the next quadrant.

BQ #3: Unit T Concept 1-3

• How do the graphs of sine and cosine relate to each of the others?  Emphasize asymptotes in your response.

Sine and cosine relate to generally all the other graphs. In tangent, tangent is equal to sin/cos. So when cosine is equal to 0 there will be an asymptote. This means there will be an asymptote at 90 degrees, pi/2 and 270 degrees, 3pi/2. At these two points tangent will have have an asymptote. For cotangent the ratio is cos/sin. So when sine is 0 cotangent will have an asymptote. In cosecant graph we know the ratio is the inverse of sine, 1/sin. So when sine is at 0 or 180 degrees there will be an asymptote for the cosecant graph. The secant graph relies on cosine to be 0 for there to be an asymptote since the ratio is 1/cos. Sine and cosine relate to the graphs because they are apart of their ratios.

• 
  

BQ #5: Unit T Concept 1-3

          Why do sine and cosine NOT have asymptotes, but the other four trig graphs do? Use unit circle ratios to explain.

Sine and cosine graphs will never have asymptotes and reason being is their unit circle ratio. The ratio for sine is y/r and for cosine it is x/r. In the unit circle we know that r will always equal 1. And we know that asymptotes are there when it is undefined which means there is a 0 as the denominator. But for sine and cosine according to the ratio it will always be over 1 keeping it from being undefined. All the other graphs may have asymptotes because their ratios are either over x or y. And it is possible for the x and y values to be 0. When any ratio is over 0 it becomes undefined creating an asymptote.

BQ #2 Unit T

How do the trig graphs relate to the unit circle?

The trig graphs relate to the unit circle with the use of the quadrants in the unit circle.For example sine is positive in quadrants 1 and 2 so the graph will be positive through pi since the end of the second quadrant is 180. As soon as the graph passes pi it becomes negative because that's where in quadrant 3 sine becomes negative. The graph will stay negative through quadrant 4, 2pi, because of the unit circle. Once the graph gets to 2 pi the graph as well as the unit circle start over. Since the pattern of this will begin again, the first whole time the graph goes through the unit circle is called a period. This is how the graph of a trig function comes from the unit circle.

Why is period for sine and cosine 2pi whereas period for tangent and contingent is pi?
This is so because sine and cosine have to go through the whole unit circle before it repeats itself again and to go around the whole unit circle is 360 degrees, or 2pi. Tangent and cotangent is only pi because in the unit circle their quadrants are positive negative positive negative. So within the first two quadrants tangent has gone through a period because after that it will already start repeating itself. The end of quadrant 2 would be 180 or pi. Leaving tangent and cotangent pi to become a period.

 How does the fact that sine and cosine have amplitudes of one (and the other trig functions don’t have amplitudes) relate to what we know about the Unit Circle?
Sine and cosine are the only trig functions that have amplitudes because these are the only ones that have restrictions. In the unit circle sine and cosine can't be greater than 1 our less than -1. All the other trig functions do not have restrictions therefore they do not contain amplitudes.