BQ #7:Unit V

 Difference Quotient

The difference quotient is a formula that finds the slope of the secant line and will help us find the slope of any given slope of a tangent line. Since the difference quotient is used for the slope, it is derived from the slope formula.

Using the slope formula of y2-y1/x2-x1, we know that the x1 and y1 is just x because that is our first point on the graph.The second point is unknown so it is x + the change in height which is h, (x+h). We now plug in the (x+h) for x2 and y2. This gives us (x+h)-y1/(x+h)-x1. In the denominator we have the x's canceling and that would leave us with (x+h)-y/h. Or (x+h)-x/h. This is how we derive the difference quotient from the slope formula.

http://s2.hubimg.com/u/5678981_f520.jpg

http://upload.wikimedia.org/wikipedia/commons/8/8c/Derivative.png

BQ #6: Unit U

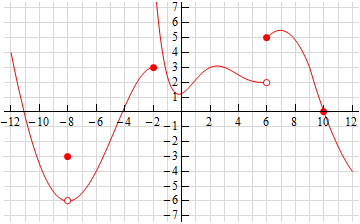
1. What is continuity? And what is discontinuity?

A continuity is a function in which on a graph is predictable, has no breaks, no holes, and no jumps, and can be drawn without lifting your pencil. While a discontinuity is the opposite, it isn't predictable, has breaks, holes, and jumps, and you must lift your pencil to draw these. A discontinuity are set in two families: removable and non removable. These are different and it will be mentioned later in this post.  In the removable discontinuities there is only one and that is the point discontinuity, this is usually known as a hole. In the non removable discontinuities there are three; the jump, oscillating, and infinite discontinuities. The jump discontinuity is when it goes from one point on a graph to another without the graph touching. An oscillating discontinuity is when the graph just becomes a bunch of wiggly lines. The infinite discontinuity is a result of a vertical asymptote.

2. What is a limit?

A limit is the intended height of a graph. The limit exists when we reach the same height from the left and right. This can only be reached if the graph is a continuity or part of the removable discontinuities. There will be no limit if the non removable discontinuities are set. With this, the limit will not exist when the graph is different from the left and the right, when there is unbounded behavior, and/or there is oscillating behavior. A limit is different from a value because the limit is only the predicted point of a function, while the value is the actual point of the function.

3. How do we evaluate limits? 

To evaluate the limit numerically we must set up a table. In this table we have the x we approach as our middle number and we get as close to that number as possible from the left and right, usually with .1, .01, .001 and .9, .99, .999. You plug the function into your calculator and trace the graph plugging in the numbers other than the middle number. To evaluate the limit graphically we must slide our fingers from the left and the right and when they get to the same height that approaches the x that is the limit. There are several ways to evaluate the limit algebraically with direct substitution, dividing out/factoring, and rationalizing/conjugate methods. In direct substitution we take the limit and plug it straight into the function. If the answer turns out to be a numerical value, 0/#, #/0 then those are the answers but if there is a 0/0 then you must look to use a different method. In factoring method, you factor both the numerator and the denominator and cancel the common terms. Once we cancel the terms we use direct substitution again for what is remaining. In the conjugate method we multiply the top and bottom by the conjugate of where usually the radical will be. When we multiply this it is just a different form of 1. So we multiply the conjugate and simplify it by foiling, but we do not multiply out the non conjugate. We do this because this is what will cancel out. After canceling our we go back to the substitution method. 

Conjugate method

http://hsmathelearnings4.wiki.hci.edu.sg/file/view/conjugate_example.jpg/204976568/328x342/conjugate_example.jpg

http://choosgs4math.wiki.hci.edu.sg/file/viewlimit_example_2.jpg/205241252/560x356/limit_example_2.jpg

http://tutorial.math.lamar.edu/problems/CalcI/Continuity_files/image002.gif

I/D1: Unit N

How do SRT and UC relate?

Inquiry Activity Summary:
In this activity we were asked to find and simplify the lengths of the special right triangles with the hypotenuse equalling 1. We must always draw the fortunate plane for each because the coordinate is derived from the unit circle.

30-60-90 SRT

Here we have the special right triangle of 30-60-90. This triangle has an original hypotenuse of (2x) a height of (x) and the length of (x rad 3). To make the hypotenuse of (2x) to equal 1 we must divide all sides of the triangle by (2x).

We divided all sides by 2x to reduce the hypotenuse equal to 1. The effect of doing this cause the length of the triangle to become rad 3/2. The height then becomes 1/2.

45-45-90 SRT

In this special right triangle we have the 45-45-90. The rules for this triangle we have the hypotenuse equal x rad 2 and both the height and length equal x.

To make the hypotenuse equal 1 we have to divide it by x rad 2. And whatever we do to one side we must do to all to keep it proportional. When we do this the height and length become rad 2/2.

60-30-90 SRT

This triangle is similar to the 30-60-90 triangle but it is in a different position. The hypotenuse is 2x the length is x and the height is x rad 3. We must do what we did to the first triangle and divide the sides by 2x.

When we divide by 2x the hypotenuse becomes 1, the length becomes 1/2, and the height is rad 3/2.

How does this activity help you to derive the Unit Circle?

This activity helps derive the unit circle because it helps us understand and know where the points of the unit circle come from. This activity also showed the way the triangles are proportioned so the hypotenuse is equal to one. 

5. 

The quadrants of the triangles shown are in quadrant one. The quadrants change the value of it is either positive or negative. In quadrant 2 x is negative and y is positive, in quadrant 3 x and y are negative, quadrant 4 x is positive and y is negative.

This triangle is in quadrant 2 and all x-values are negative.

In this it shows a triangle in quadrant and all values are negative.

This triangle is located in quadrant and all y values are negative in this quadrant.

INQUIRY ACTIVITY REFLECTION

The coolest thing I learned from this activity was that these triangles are the only ones that have these special rules.

This activity will help me in this unit because it will help me understand the unit circle and how the quadrants can affect the triangle and which points are positive and negative.

Something I never realized before about special right triangles and the unit circle is that the quadrant affects the negative and positive of a point. And that the triangles have special rules that only apply to these specific triangles.

BQ #4: Unit T Concept 3

• Why is a “normal” tangent graph uphill, but a “normal” Cotangent graph downhill? Use unit circle ratios to explain.
• 
• 
  
• A cotangent and tangent have goes different ways because of their ratios. Cotangent with x/y and tangent with y/x. These affect the graphs because it determines where the asymptotes will be. In a tangent graph when sine is 0 there will be an asymptote and when cosine is 0 there will be an asymptote for the cotangent graph. In the unit circle the quadrants are exactly the same but the ratio changes the graph. In quadrant 1 they are both positive but since sine is 0 at 90 degrees the tangent graph needs to go uphill in order to follow the unit circle of being positive and get near the asymptote. For the cotangent graph the asymptote is at 0 so the graph needs to start up near the asymptote to be positive then go downhill to be negative in the next quadrant.

BQ #3: Unit T Concept 1-3

• How do the graphs of sine and cosine relate to each of the others?  Emphasize asymptotes in your response.

Sine and cosine relate to generally all the other graphs. In tangent, tangent is equal to sin/cos. So when cosine is equal to 0 there will be an asymptote. This means there will be an asymptote at 90 degrees, pi/2 and 270 degrees, 3pi/2. At these two points tangent will have have an asymptote. For cotangent the ratio is cos/sin. So when sine is 0 cotangent will have an asymptote. In cosecant graph we know the ratio is the inverse of sine, 1/sin. So when sine is at 0 or 180 degrees there will be an asymptote for the cosecant graph. The secant graph relies on cosine to be 0 for there to be an asymptote since the ratio is 1/cos. Sine and cosine relate to the graphs because they are apart of their ratios.

• 
  

BQ #5: Unit T Concept 1-3

          Why do sine and cosine NOT have asymptotes, but the other four trig graphs do? Use unit circle ratios to explain.

Sine and cosine graphs will never have asymptotes and reason being is their unit circle ratio. The ratio for sine is y/r and for cosine it is x/r. In the unit circle we know that r will always equal 1. And we know that asymptotes are there when it is undefined which means there is a 0 as the denominator. But for sine and cosine according to the ratio it will always be over 1 keeping it from being undefined. All the other graphs may have asymptotes because their ratios are either over x or y. And it is possible for the x and y values to be 0. When any ratio is over 0 it becomes undefined creating an asymptote.

BQ #2 Unit T

How do the trig graphs relate to the unit circle?

The trig graphs relate to the unit circle with the use of the quadrants in the unit circle.For example sine is positive in quadrants 1 and 2 so the graph will be positive through pi since the end of the second quadrant is 180. As soon as the graph passes pi it becomes negative because that's where in quadrant 3 sine becomes negative. The graph will stay negative through quadrant 4, 2pi, because of the unit circle. Once the graph gets to 2 pi the graph as well as the unit circle start over. Since the pattern of this will begin again, the first whole time the graph goes through the unit circle is called a period. This is how the graph of a trig function comes from the unit circle.

Why is period for sine and cosine 2pi whereas period for tangent and contingent is pi?
This is so because sine and cosine have to go through the whole unit circle before it repeats itself again and to go around the whole unit circle is 360 degrees, or 2pi. Tangent and cotangent is only pi because in the unit circle their quadrants are positive negative positive negative. So within the first two quadrants tangent has gone through a period because after that it will already start repeating itself. The end of quadrant 2 would be 180 or pi. Leaving tangent and cotangent pi to become a period.

 How does the fact that sine and cosine have amplitudes of one (and the other trig functions don’t have amplitudes) relate to what we know about the Unit Circle?
Sine and cosine are the only trig functions that have amplitudes because these are the only ones that have restrictions. In the unit circle sine and cosine can't be greater than 1 our less than -1. All the other trig functions do not have restrictions therefore they do not contain amplitudes.

Reflection #1 - Unit Q

24. What does it actually mean to verify a trig identity?
        
      To verify a trig function is to make sure the equation is true by having both sides equal to each other. In order to do this we must not touch the right side of the equal sign. We must use identities to change the equation and find something to cancel out. Verifying a trig function is making both sides of equal sign look identical. 

25.What tips and tricks have you found helpful?

     A trick I have found helpful is looking for the cosine and sines to change into. Doing this makes it easier to change it into another function. It is also helpful to label the steps you are doing because it will help know where you are in the problem. And re-watch videos that you don't understand. Things make more sense when it's explained the second time. 

26.Explain your thought process and steps you take in verifying a trig identity. 

     My thought process looks for a trig function that can be changed in to either cosine or sine. If there is no possible way to do this then I will look for any other identity to replace the original function. If the function is complicated I will seek to split them apart such as (1/tanxsinx • secx/1). In this we split the original equation of secx/tanxsinx. After looking to split the functions I will see if there is any possible way to cancel anything out. This will lead to verifying the trig function. 

I/D3: Unit Q - Pythagorean Identities

Pythagorean Identities

We know that an identity is always true. So this makes the Pythagorean Theorem an identity, with a^2+b^2=c^2. We replace a,b, and c with x,y, and r making x^2+y^2=r^2. We need to make the theorem equal to 1. We do this by dividing everything by r. Our equation is now (x/r)^2+(y/r)^2=1. From our unit circle we know the ratio of cosine is x/r which means we can substitute cos for x/r. The ratio for sine from the unit circle is y/r and now we can plug in sin for y/r. Plugging both of these in gets us cos^2x+sin^2x=1 which is our main identity.

To derive the identity with secant and tangent from cos^2x+sin^2x=1 we must divide everything by cos^2. We now have sin^2x/cos^2x=1/cos^2x. From the Ratio identity we know tanx=sinx/cosx therefore we are able to plug in tan^2x for sin^2x/cos^2x. We are able to do this because the ratio identities are allowed to power up. As for the other side we know from the Recipricol identity that secx=1/cosx. The Reciprical identity is also allowed to power up, the only one not allowed to is the pythagorean identity. So now we are left with the final identity of 1+tan^2x=sec^2x.

To derive the identity with cosecant and cotangent we must divide everything by sin^2x. Giving us cos^2x/sin^2x+1=1/sin^2x. In the ratio identity cotx=cosx/sinx and even though the problem is squared the ratio identities are allowed to be powered up allowing it to be cot^2x to equal cos^2x/sin^2x. The reciprical identity says that cscx=1/sinx. This identity is also allowed to be powered up, so it equals csc^2x=1/sin^2x. The final equation is cot^2x+1=csc^2x. 

   INQUIRY ACTIVITY REFLECTION

The connections I see between units N, O, P, and Q are that they all use the trig functions in some way. They are also the same because it is all derived from the unit circle.

If I had to describe trigonometry in three words, they would be, simple once learned.

WPP #13 & 14: Unit P Concept 6 & 7

WPP 13 & 14 Unit P Concept 6&7

This WPP was made in collaboration with Daniel. Please visit the other awesome posts on their blog by going here.

Blake and Steve both see a ball. They get 3 miles apart east and west of each other to race to the ball. Blake runs at a bearing of 050* at 20 mph for 15 min to get to the ball. How far away is Steve away from the ball?

Law of Cosines

Once Blake gets to the ball he throws it at a bearing of N 25 W with a distance of .8 miles. When it lands Steve looks at the at a bearing of N 70 W. How far apart are Blake and Steve? 

BQ#1 - Unit P

BQ#1 - Unit P 

1. Law of Sines - Why do we need it?  How is it derived from what we already know?  

Here we have the non-right triangle and once we make a line straight down from B we get two right triangles and could use what we know with the trig functions.

To derive the Law of Sines we know that to get A we need to use Sine and get the opposite/hypotenuse giving us h/c. We multiply both sides by c to get h by itself. And now have cSinA=h. We must also do the same to get C. Taking the same steps as A, we will get aSinC=h. Since both equal h, this means they both equal each other, cSinA=aSinC. We now need to get SinA and SinC by themselves, so we divide both sides by ac. And c will cancel out on one side and a will cancel out on the other leaving us with SinA/a=SinC/c

1. 1. 
      
   
   4. Area formulas - How is the “area of an oblique” triangle derived?  How does it relate to the area formula that you are familiar with?
   
   We derive this formula because we first know the original equation is A=1/2bh. We dont know the h so to find this we must use the trig functions. We know that the SinC=h/a and to get h by itself we multiply each side by a. We now replace h with aSinC giving us A=1/2b(aSinC).
   
   
   This relates to the original area formula because we are using the exact same formula except replacing h because in order to find h we must use the trig function. And instead of just finding h and plugging it in, we plug in the trig function to find h in the original equation.

WPP #12: Unit O Concept 10

WPP #12: Unit O Concept 10

David is about to jog a a hill. The hill has a 25 degree elevations and is 46 feet high. What is the length he'd run to the top?

David gets to the top of the hill and takes a break. As he looks he sees the other side of the hill is much steeper with an angle depression of 32 degrees, he also sees a lone tree that is about 92 feet on the trail down. What is the length of the horizontal line from top of hill to the tree?

I/D #2: Unit O - Derive the SRTs

INQUIRY ACTIVITY SUMMARY

45-45-90

        

      To create a 45-45-90 triangle we must cut the square diagonally. Cutting the square diagonally will cut two of the 90 angles in half creating a 45 angle. To find the hypotenuse we must use the Pythagorean theorem. Since we know 'a' and 'b' we can plug that into the equation of a^2+b^2=c^2. Once we plug in 1 and 1 we get 2=c^2. We must get 'c' by itself and doing so by getting the square root of it canceling out the power of 2. What we do to one side we must do to the other and this gives us the 'square root of 2=c' and we now have the hypotenuse of 'square root of 2.'  We use 'n' on each side because the relationship between all 45-45-90 triangles would be the same. 

30-60-90

   

        To create the special right triangle of 30-60-90 we must cut an equilateral triangle right down the center. We do this to create two triangles and it divides the top 60 angle in half and creates a 30 angle in each triangle. Doing this also makes the 90 angles at the bottom of the triangle. Put it all together and we have the 30-60-90 triangle. Since the bottom length of the triangle was 1 cutting the triangle down the middle makes it 1/2 in both triangles. To get the height of the triangle we must use the Pythagorean theorem. a=1/2 and c=1 leaving us to find 'b', the height. Since a=1/2 we will multiply all sides by 2 to get rid of the 1/2. The equation will now be 1^2+b^2=2^2. After we solve for 'b' we will get the 'square root of 3' as the height. We again use 'n' to show the relation between all 30-60-90 triangles and how they each will have the same variables such as 2n,n, and n|3. 

 INQUIRY ACTIVITY REFLECTION

       Something I never noticed before about special right triangles is that every special right triangle will have the same relations no matter what the lengths of the triangle are.

Being able to derive these patterns myself aids in my learning because now I completely understand where the variables come from and it makes more sense of what I am doing when I am solving for problems that involve this.

RWA1: Unit M Concepts 4-6 - Conic Sections in real life.

http://www.youtube.com/watch?v=lvAYFUIEpFI

http://www.mathsisfun.com/geometry/ellipse.html

1. An ellipse is the set of all points on a plane whose distance from two points add up to be a constant

2. The equation algebraically is (x-h)^2/a^2+(y-k)^2/b^2=1

     An ellipse is almost like a smashed circle. (as shown above)

     To find the standard form we must use the center point of the ellipse and plug it into the equation.(x,y)=(h,k). If the ellipse is skinny a^2 goes under y and if its fat a^2 goes under x. the major axis is the longest diameter of the ellipse and the minor axis is the shortest. To find a you would find the number from one of the vertices to the center of the ellipse. To find b you would find the distance from one of the covertices to the center. To find c we would have to use a^2-b^2=c^2. To find the eccentricity we put c over a and it should be less than 1. If you place the foci farther away from the center the wider the ellipse will get. 

3. Conic sections are used everyday in the real world. They may not seem huge but they make an important difference. One example is with tanks that carry heating oil or gasoline. The tanks are never circular but rather elliptical. "This gives them a high capacity, but with a lower center-of-gravity, so that they are more stable when being transported." (http://mathforum.org/library/drmath/view/62576.html) If the tank was a circle then its height would be greater and it wouldn't fit under bridges. Without an elliptical tank things like oil and gasoline would be much harder to transport.

     These conic sections also get things going such as bicycles. The gear that connects to the pedal crank is basically an elliptical shape. "Here the difference between the major and minor

  axes of the ellipse is used to account for differences in the speed and force applied"(http://mathforum.org/library/drmath/view/62576.html)

With this elliptical shape your legs are able to push and pull more effectively. Conic sections are used everyday in the real world with things that are the least noticeable yet make the biggest differences. A world without conic sections would be difficult.

4. References:

. http://mathforum.org/library/drmath/view/62576.html

. http://www.mathsisfun.com/geometry/ellipse.html

. http://www.youtube.com/watch?v=lvAYFUIEpFI

. http://www.mathopenref.com/ellipseaxes.html

. http://www.mathopenref.com/ellipsefoci.html 

WPP 6: Unit I Concept 3-5

Create your own Playlist on LessonPaths!

WPP 10 Unit L Concept 9-14

Create your own Playlist on LessonPaths!